"Die Volatilitätsrisikoprämie bei Futures: Das Geschäft mit der Angst"

Bisher haben wir nur den Zusammenhang zwischen dem VIX und den realisierten Volatilitäten betrachtet, um daraus die VRP bei Optionen abzuleiten. Doch was spielt sich darüber hinaus auf der Terminstrukturkurve des VIX ab?

Grundsätzlich stellen Futures-Märkte ein Nullsummenspiel dar, weil es für jede Long- auch eine Short-Position gibt. Jeder Futures-Kontrakt ist damit die beste Schätzung des Marktes, wo sich der VIX zum entsprechenden zukünftigen Verfallszeitpunkt befinden wird. Das Problem dabei: Der prognostizierbare Anteil der künftigen Volatilitätsveränderungen am Markt ist bei Futures bereits eingepreist. Sind die Volatilitäten aktuell sehr niedrig und lässt sich prognostizieren, dass sie in Zukunft eher steigen (siehe Teil 1 dieser Artikelserie in TRADERS´ 07/2018), so ist dies anhand sukzessive höherer Futures-Preise für längere Laufzeiten (Contango) der Fall.

Umgekehrt liegen die Futures für längere Laufzeiten sukzessiv niedriger (Backwardation), wenn die Volatilitäten momentan sehr hoch sind und sich prognostizieren lässt, dass sie eher fallen werden. Der Futures-Markt ist also sehr effizient und es sollte schwierig sein, hier eine Prämie rauszuholen.

Die VRP bei Futures

Es stellt sich also die Frage, ob bei Futures überhaupt eine zusätzliche VRP existiert. Um das herauszufinden, lassen sich zum Beispiel der Frontmonats- sowie der nächstfällige Future so gewichten, dass deren Kombination stets eine mittlere Fälligkeit in 30 Tagen repräsentiert. Dies stellt fortlaufend die Erwartung des Marktes dar, wo der VIX in 30 Tagen stehen wird. Diese Schätzungen basieren oft auf der aktuellen Terminstrukturkurve des VIX, die Aufschluss über zukünftige Volatilitätserwartungen gibt. Nun können wir analog zur Vorgehensweise bei der Options-VRP vergleichen, wo der VIX tatsächlich jeweils 30 Tage später steht. Auch diese Berechnungen hat Tony Cooper angestellt und in seinem Paper veröffentlicht (siehe Bilder 1 und 2). Dabei stellt sich heraus, dass auch die Futures eine kleine VRP aufweisen – also im Durchschnitt etwas zu hoch notieren und damit die künftigen VIX-Stände überschätzen.

B1 Volatilitätsrisikoprämie bei Futures

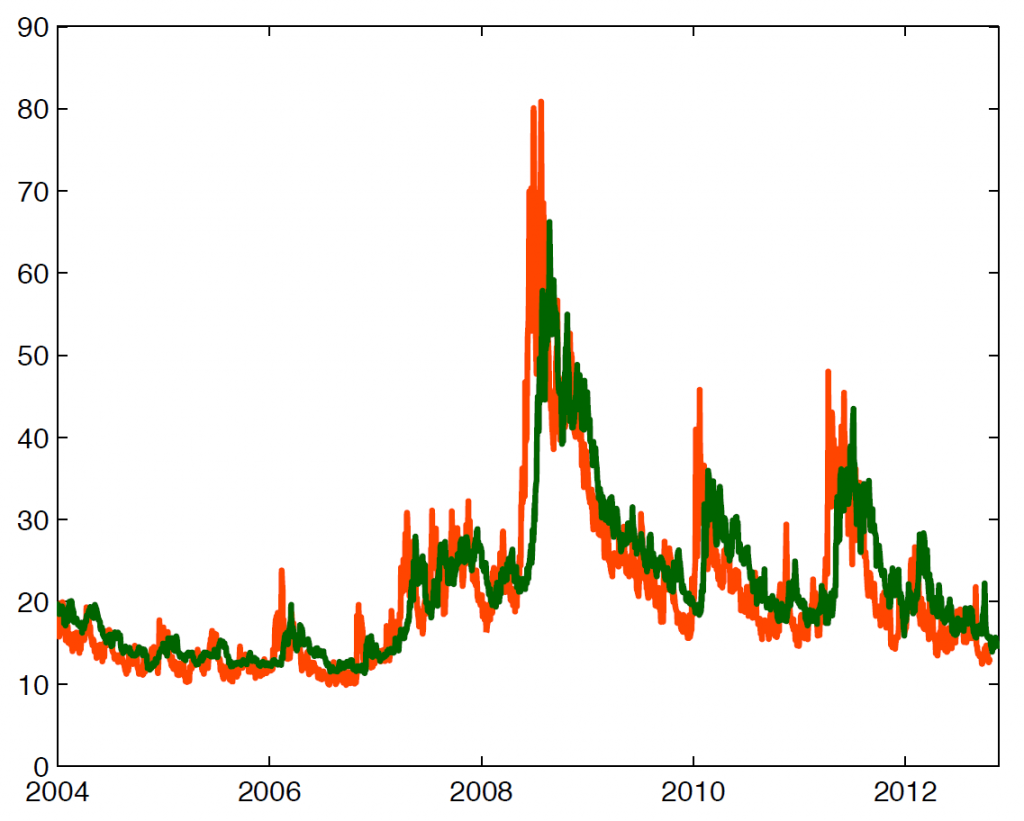
Die Grafik zeigt, dass die gewichteten VIX-Futures für eine Fälligkeit in 30 Tagen (grüne Linie) im Durchschnitt etwas höher liegen als die mittleren realisierten VIX-Werte 30 Tage nach dem jeweiligen Beobachtungstag. Diese Differenz repräsentiert im Durchschnitt die VRP der Futures.

Quelle: Cooper, T. (2013), Easy Volatility Investing, Double-Digit Numerics, S. 7

B2 Futures-VRP im Zeitablauf

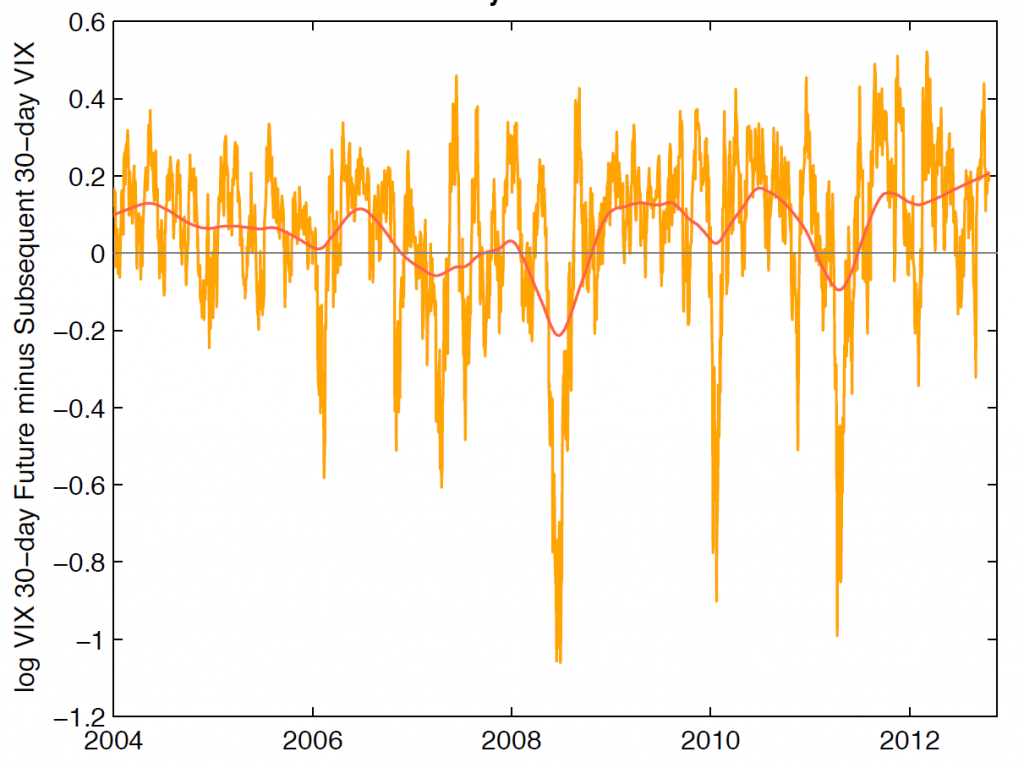
Bild 2 zeigt die Differenz der beiden Linien aus Bild 1. Dabei wurde mit logarithmierten Werten gerechnet, um zu große Spikes zu vermeiden. Es ist gut zu erkennen, dass die VRP vor allem in turbulenten Marktphasen auch deutlich negativ sein kann, was die mittlere langfristige Prämie deutlich belastet. Demgegenüber ist die im letzten Teil dieser Artikelserie vorgestellte VRP bei Optionen insgesamt attraktiver.

Quelle: Cooper, T. (2013), Easy Volatility Investing, Double-Digit Numerics, S. 7

Um die Futures-VRP zu vereinnahmen, können Trader systematisch VIX-Futures verkaufen und die Positionen bis zur Fälligkeit halten. Die so im Zeitablauf erzielte Prämie stammt von der Gegenseite, den Long-Positionen in VIX-Futures. Dabei nimmt die relative VRP in der Regel ab, je weiter man sich auf der Terminstrukturkurve des VIX in die Zukunft bewegt.

Woher stammt die VRP bei Futures?

Ähnlich wie bei der VRP für Optionen stellt sich auch bei der für Futures die Frage, warum sie überhaupt existiert. Grundsätzlich scheint es auch hier ein Ungleichgewicht von Angebot und Nachfrage nach Absicherungs- und Spekulationsinstrumenten zu geben. Zum einen dominieren am Markt die institutionellen und privaten Anleger, die sich mit Long-Positionen in VIX-Futures gegen fallende Kurse absichern oder direkt auf stark steigende Volatilitäten spekulieren möchten. Zum anderen ist es so, dass auch bei VIX-Futures ein asymmetrisch höheres Risiko für Short-Positionen besteht. In der Regel fallen die Kurse am Aktienmarkt viel schneller als sie steigen, was sich in schnellen, starken Spikes im VIX und seinen Futures niederschlägt. Zudem können die Verluste bei Short-Positionen deutlich höher ausfallen, da der VIX als Basiswert um mehr als 100 Prozent steigen, aber nur begrenzt weit fallen kann.

Die oft geäußerte Vermutung, dass die VRP bei Futures aus den Rollvorgängen resultiert, ist allerdings falsch. Denn sowohl der Future als auch der VIX selbst sind im Zeitablauf bewegliche Größen, die zum Verfall hin von beiden Seiten gegeneinander konvergieren können. Strategien, die auf der Rollrendite basieren, sind vor allem deshalb oft erfolgreich, weil die Rollrenditen mit der VRP korrelieren. Der Vorteil der Rollrenditen ist dabei, dass sie anhand der Terminstruktur klar messbar sind. Die wahre Renditequelle, nämlich die VRP, ist dagegen erst bekannt, wenn der entsprechende Future verfällt und zum dann aktuellen VIX-Stand gesettelt wird.

Szenario-Rechnungen

Wenn die Terminstrukturkurve steigend verläuft (Contango), was die meiste Zeit der Fall ist, so rechnen die Marktteilnehmer mit künftig höheren Volatilitäten. Doch die VIX-Futures setteln erst beim Verfall zum dann tatsächlich gegebenen VIX-Stand. Das kann bedeuten, dass sie bis dahin entsprechend fallen, wenn der VIX weiterhin niedrig notiert. Umgekehrt kann der VIX aber auch stärker steigen, als es die Erwartung der jeweiligen Futures zum Einstiegszeitpunkt anzeigte und so zu steigenden Futures führen. Dazwischen treten häufig Szenarien auf, in denen VIX und Futures gegeneinander konvergieren.

Ein grundsätzlicher Effekt ist, dass die VIX-Futures dem VIX nicht im Verhältnis 1:1 folgen. Dazu ein vereinfachtes Rechenbeispiel. Angenommen, wir haben eine typische Contango-Situation in einem Bullenmarkt, wie sie die meiste Zeit im Jahr 2017 zu beobachten war:

- realisierte Volatilität der letzten 30 Handelstage: 12 Prozent
- erwartete Volatilität der nächsten 30 Handelstage (VIX): 15 Prozent
- Frontmonat-VIX-Future (noch 15 Tage Laufzeit): 18 Prozent
- darauffolgender VIX-Future (noch 45 Tage Laufzeit): 20 Prozent

Wenn man also heute den Frontmonat des VIX-Futures bei 18 shortet und der VIX in 15 Tagen noch unverändert bei 15 notiert, entsteht ein Gewinn in Höhe von 15 / 18 = 17 Prozent. Shortet man dagegen den darauffolgenden Kontrakt bei 20 und notiert der VIX in 45 Tagen noch immer unverändert bei 15, entsteht ein Gewinn in Höhe von 15 / 20 = 25 Prozent.

Betrachten wir nun den umgekehrten Fall, nämlich einen Crash am Aktienmarkt, der den VIX um 200 Prozent ansteigen lässt. Vollzieht der VIX-Future-Frontmonat das zu 50 Prozent und der darauffolgende Kontrakt zu 30 Prozent nach, ergibt sich folgende Rechnung:

- VIX notiert bei 45
- Frontmonat-VIX-Future notiert bei 36
- darauffolgender VIX-Future notiert bei 32

Plötzlich haben wir eine umgekehrte Situation: Die Terminkurve verläuft jetzt fallend (Backwardation) und die Marktteilnehmer rechnen mit niedrigeren Volatilitäten. Wenn man nun den Frontmonats-Future bei 34 glattstellt, entsteht ein Verlust in Höhe von 34 / 18 = minus 89 Prozent. Hatte man den darauffolgenden VIX-Future bei 20 geshortet, beträgt der Verlust 32 / 20 = minus 60 Prozent.

Auf den ersten Blick schneidet der länger laufende Future im Verlustfall also besser ab, da er sowohl beim Einstieg höher als auch beim Ausstieg niedriger als der Frontmonat lag. Doch diese Einschätzung trügt, denn wir müssen auch das um 30 Tage längere Risiko-Zeitfenster berücksichtigen.

Findet der Crash nämlich nicht wie vorhin angenommen schon in den nächsten Tagen statt, sondern erst in einem Monat, so würde man im Frontmonat wie oben berechnet 17 Prozent Gewinn erzielen (wenn Settlement bei 15, bevor der Crash beginnt); der darauffolgende Kontrakt, der in einem Monat dann der neue Frontmonat ist, ist dagegen vom Crash betroffen und weist wie schon berechnet einen Verlust von 60 Prozent auf.

Fazit

Es gibt zwei verschiedene Volatilitätsprämien. Die erste ist der Betrag, den der VIX höher liegt als die später tatsächlich realisierte Volatilität. Trader können diese Prämie vereinnahmen, indem sie fortlaufend Stillhalterpositionen in Optionen eingehen und halten. Die zweite ist der Betrag, den ein Futures-Kontrakt über dem VIX liegt, zu dem er am Ende seiner Laufzeit gesettelt wird. Trader können diese Prämie vereinnahmen, indem sie fortlaufend Short- Positionen im Future eingehen und halten. Tony Cooper schreibt, dass die Korrelation zwischen der VRP bei Optionen und Futures in seinem Betrachtungszeitraum nur 0,56 beträgt. Beide Prämien bewegen sich also nicht genau gleich; es handelt sich tatsächlich um zwei verschiedene Effekte.

Insgesamt können wir festhalten, dass die VRP bei Optionen attraktiver ist als die VRP bei Futures. Der „Haken“ beim Vereinnahmen der Prämien ist jeweils, dass man mit beweglichen Größen hantiert, die sich während der notwendigen Haltedauer erheblich verändern können. Es handelt sich bei der VRP also nicht um eine bloße Anomalie oder gar ein „Free Lunch“, sondern um eine Kompensation für das eingegangene und über die Zeit ausgehaltene Risiko.

Der Original-Artikel erschien in der Ausgabe 10.2018 im Magazin TRADERS´. Da es sich um einen historischen Beitrag handelt, können sich Personen-, Firmen- und Produktdaten, Webseiten, Software, Strategien, Marktphasen, gesetzliche Regelungen und anderes verändert haben bzw. ungültig geworden sein. Die Aktualität des Artikels bezieht sich somit stets auf das Erscheinungsdatum.

• Lesen Sie einen weiteren interessanten Artikel zum Thema:  Profitieren sie vom Expertenwissen: Hier finden sie einen Vorteil beim Börsenhandel
• Folgen Sie der Traders-Mag Gruppe auf TradersYard…
• Informieren Sie sich über die neuesten Ausgaben des Traders-Magazine…
• Melden Sie sich zu den TradersMag Daily-Briefings an…

Featured by TradersYard und AgenaTrader